
Juros compostos são essenciais no mercado financeiro, mas você sabe como eles funcionam e como utilizá-los a seu favor? A utilização do juros é bastante comum em transações financeiras, principalmente em compras parceladas.
Empréstimos, pagamento de contas, e cartão de crédito são influenciados pelos juros compostos, então é muito importante que você saiba como calculá-los. Neste guia do InvestNews vamos te explicar o que são juros compostos, qual é a fórmula de cálculo, como calculá-los e como utilizá-los a seu favor.
Caso esteja com pressa, preparamos para você um resumo rápido no final da página.
Fórmula dos Juros Compostos:
Juros compostos são baseados em um regime de juros acumulado no qual o montante é calculado a partir do montante anterior (um valor já corrigido pelos juros), ou seja, incidindo também sobre esses juros. Para entender como funciona, é essencial que você saiba qual é a fórmula para calculá-lo.
M = C*(1+i)t
- C – capital inicial: valor de referência no início da operação, o valor presente, atual
- i – taxa: taxa de juros utilizada na operação
- t: tempo: tempo de aplicação daquela taxa sobre o valor investido
- M – montante: valor final, resultado obtido após a soma do seu capital com o valor obtido do juros.
*Importante: simplificadamente, porcentagem é a divisão de qualquer número por 100, certo? Então, se temos 100% de um valor, temos 100/100 = 1. Quando estamos calculando um valor que excede o meu capital atual, consideramos no cálculo o número 1, que representa esses 100%, e se somado à taxa daquela operação, resulta na porcentagem final do processo, como pode ser observado abaixo, no cálculo de juros compostos.
Cálculo de juros compostos
Para facilitar, vamos utilizar valores “arredondados” e mais fáceis de calcular, meramente ilustrativos.
Temos um investimento cujo valor de aplicação é de R$ 1.000, sob a taxa de juros de 2% ao ano, por 4 anos.
Encaixando os valores na fórmula de juros compostos, temos:
- Capital (C) = R$ 1.000
- taxa de juros (i) = 2% a.a (ao ano)
- tempo (t) = 4 anos
- Montante (M) = é o valor que iremos calcular
M = 1.000*(1+0,02)4
M = 1.0882,4322
Observe:
| tempo (t) | Capital (C) | Taxa de juros (i) | Montante (M) |
| 1 | 1.000 | 2% ou 2/100 ou 0,02 2% de 1.000 = 20,00 |
= 1.000*(1+0,02) = 1.000*(1,02)1 ou 1.000 + 20 = 1.020 |
| 2 | 1.020,00 | 2% ou 2/100 ou 0,02 2% de 1.020 = 20,4 |
= 1.000*(1+0,02) = 1.000*(1,02)2 ou 1.020 + 20,4 = 1.040,40 |
| 3 | 1.040,40 | 2% ou 2/100 ou 0,02 2% de 1040,40 = 20,80 |
= 1.000*(1+0,02) = 1.000*(1,02)3 ou 1.040,40 + 20,80 = 1.061,2080 |
| 4 | 1.061,2080 | 2% ou 2/100 ou 0,02 2% de 1.061,20 = 21,22 |
= 1.000*(1+0,02) = 1.000*(1,02)4 ou 1.061,20 + 21,22 = 1.082,43 |
O capital é sempre alterado, pois o montante da operação anterior passa a ser o capital da nova operação.
Considerando que o montante é o meu valor atual (capital) somado à quantia de juros recebidos, temos a seguinte forma de resolução para encontrar o valor total do juros, quando conhecemos o montante e o capital inicial:
M = C + J
Agora você já sabe fazer cálculo de juros compostos, mas existem ferramentas que podem facilitar, e muito, a nossa vida, como calculadoras de juros compostos que você encontra no google.
O que são juros compostos
Os juros compostos são juros com crescimento exponencial, ou seja, se multiplicam muito rapidamente e por um valor constante, sendo calculados com base no montante anterior, como podemos ver nos exemplos acima. Quanto mais o capital aumenta, mais o juros cresce (o valor de diferença entre o montante e o capital).
Vamos colocar o exemplo anterior em um gráfico, observe a curva de crescimento:
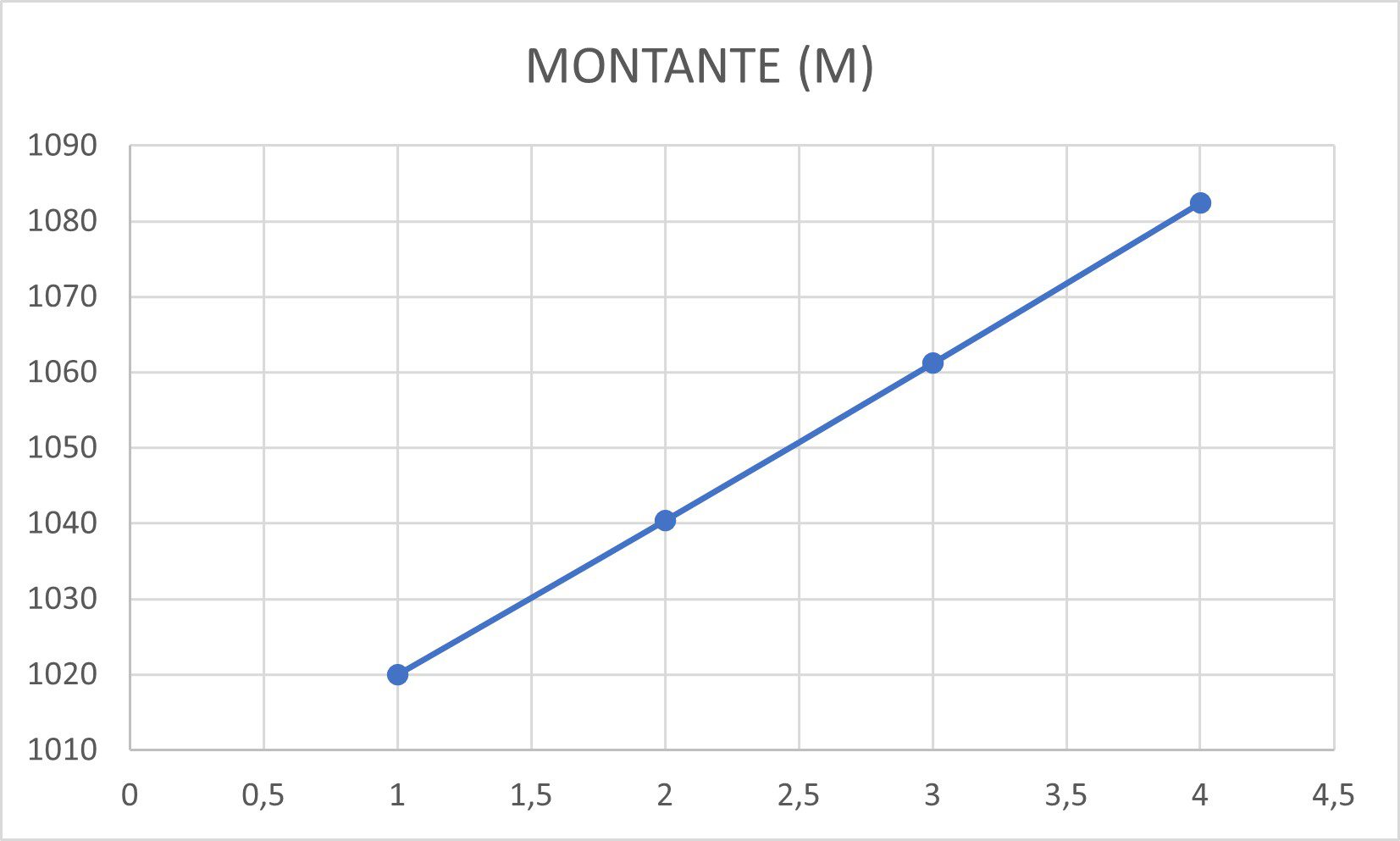
A alíquota dos juros, de 2%, não se altera. Mas conforme o capital aumenta, o montante cresce exponencialmente. Para você entender melhor, vamos demonstrar a diferença entre os juros simples e compostos.
Juros simples X juros compostos
A principal diferença entre os juros simples e compostos está na velocidade e no tipo de crescimento do valor. Mas por quê?
Os juros servem para corrigir determinado valor numa operação, seja ela um empréstimo, investimento ou compra parcelada, por exemplo.
No caso dos juros simples, a correção é sempre feita com base no valor inicial. Já os juros compostos utilizam valores já corrigidos anteriormente pelos juros.
Observe a fórmula do juros simples:
M = C + J onde J = C*i*t
*Considere J o valor do juros, e não uma alíquota.
Utilizando os mesmos dados do exemplo anterior, temos:
- Capital (C) = R$ 1.000
- taxa de juros (i) = 2% a.a (ao ano)
- tempo (t) = 4 anos
- Montante (M) = é o valor que iremos calcular
Primeiro, calculamos o valor do juros:
J = 1.000*0,02*4
J = R$ 80,00
Agora o montante:
M = 1.000 + 80
M = R$ 1.080,00
Observe a diferença de crescimento entre os valores corrigidos com base no juros simples e composto:
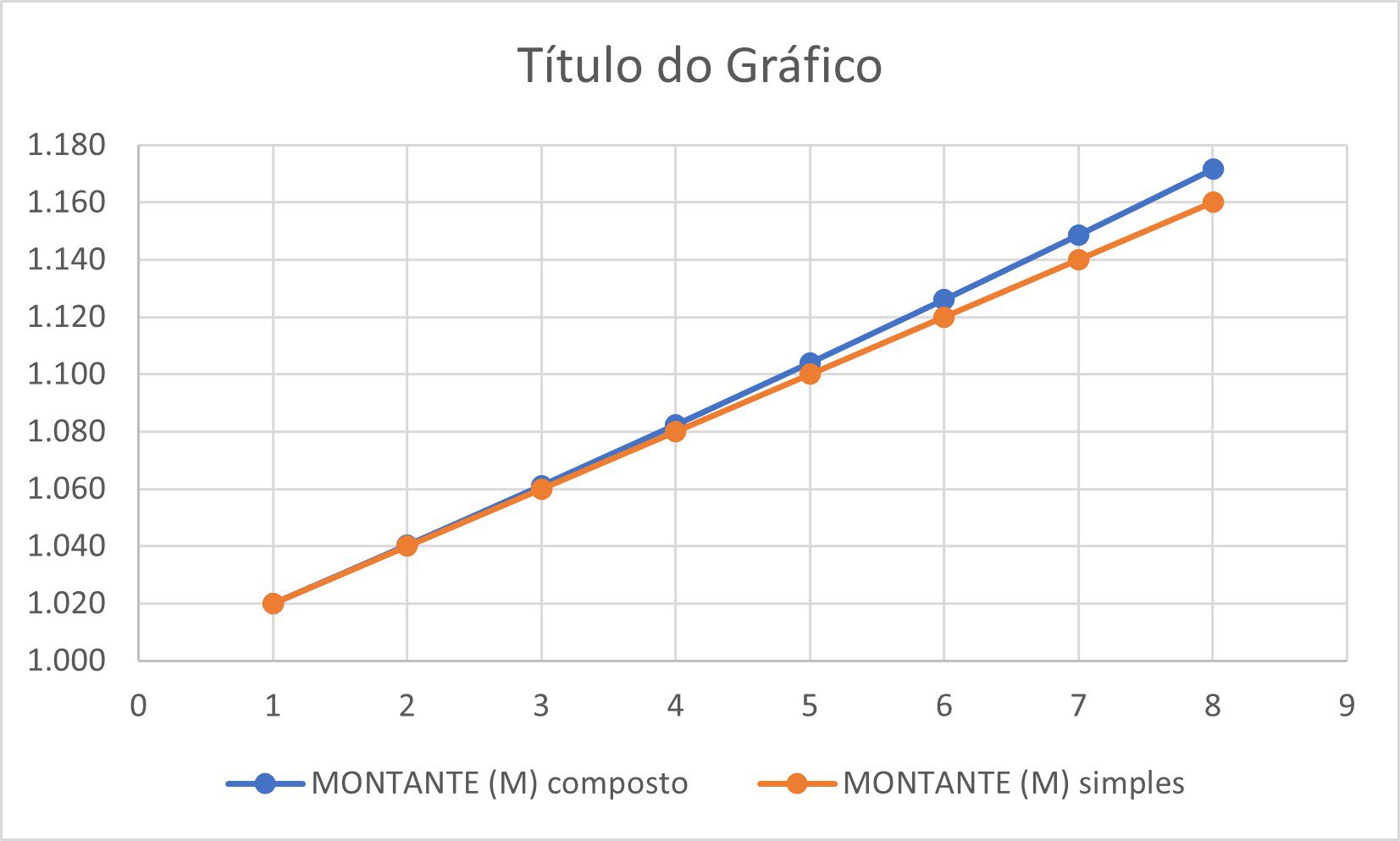
Enquanto os juros simples aumentam o valor de forma mais lenta e proporcional, os juros compostos aumentam de forma exponencial. Com o passar do tempo, maior é seu crescimento e a diferença entre os cálculos.
Como usar os juros compostos a seu favor?
Agora que você percebeu a diferença que os juros compostos podem ter na correção de um valor, como utilizá-los a seu favor?
Assim como o cartão de crédito e o empréstimo, os investimentos também são calculados com base em juros compostos, e essa é uma grande vantagem. São os juros compostos que determinam a rentabilidade que cada ativo pode fornecer, então saber o que eles são e como calculá-los já coloca você um passo mais perto de se tornar investidor.
Para quem não tem um bom controle e planejamento financeiro, os juros composto não são benéficos, mas no mercado financeiro eles se tornam um dos principais aliados dos investidores. Aqui você pode conferir um conteúdo para iniciantes sobre como investir em ações.
Aprenda em poucos minutos
- juros compostos são juros que incidem sobre um valor já corrigido por juros (montante), então são baseados em juros acumulados (juros sobre juros)
- A fórmula para cálculo dos juros é: M = C*(1+i)t
- Capital é o valor inicial da operação, (i) é a taxa de juros utilizada, (t) é o tempo de aplicação da taxa e M é o montante resultante do capital corrigido pelo juros
- O juros composto pode ser um vilão no caso de atraso de algum pagamento, como do cartão de crédito, mas ele pode ser seu aliado nos investimentos.
Veja também:
- Confira qual o retorno do seu dinheiro com a calculadora de investimentos.


